the others/Algorithm
자바스크립트 Math.sqrt( ) 사용하지 않고 제곱근 구하기
ciocio
2021. 8. 17. 23:44
📌 바빌로니아 방법 Babylonian method
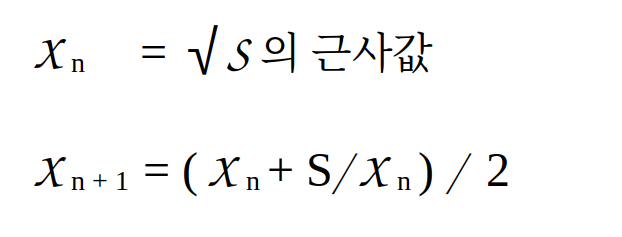
어떤 값을 넣든지 점화식을 반복하다보면 결국, Xn+1이 S의 제곱근에 근접하는 순간이 온다. (그치만 그게 언제일지는 보장못함)
📌 코드로 구현하기
◾ 초기안

수도 코드
◾ 코드 구현

값은 잘 나오는데 ...
구체적으로 코드가 어떻게 구동하는 지 궁금했다.




◾ 문제점
근사값이 점점 원래값의 제곱근에 가까워지는 걸 확인할 수 있었다.
그런데 ... 근사값은 결국 3.xxxxxxxxxxx 형식을 넘지 못한다.
그리고 9같이 제곱근이 정수로 떨어지는 숫자 이외의 값을 입력받으면 while문이 무한반복될게 뻔하다.
무한반복을 끊어줄 break문이 필요하고, -> break
그 조건은 소수점 자리수를 지정해 그 값을 끊어 계산할 필요성을 느꼈다. -> .toFixed(소수점 자리수)

소수점 자리와 상관없이 값은 같다고 나오니 ok ok

그런데 toFixed( ) 메소드는 왜 문자열을 반환하고 난리 ... 숫자로 변환해줘야한다. -> Number( )
◾ 문제 해결 코드

와아아아아아아아
Math.sqrt( ) 안쓰고도 제곱근을 구할 수 있는 함수를 만들어냈다 ~!~!~!
수도코드 쓰면서 하나 하나 구현해나가니까 되는구낭 올레
◾ 최종 코드
// Math.sqrt() 안쓰고 제곱근 구하기 코드
function makeSquareRoot(num){
let approxNum = num / 2;
while((approxNum ** 2) !== num){
if(Number((approxNum ** 2).toFixed(2)) === num){
break;
}
approxNum = (approxNum + (num / approxNum)) / 2;
}
return Number(approxNum.toFixed(2));
}
반응형